Starfish Tutorial Part 5: Collisions and Chemical Reactions

Introduction

Welcome to the final part of the Starfish tutorial. In the past lessons, we set up the computational domain, specified the potential solver parameters, added ion source, and included surface recombination. However, we have not yet considered gas interactions. The individual ion and neutral particles were able to pass right through without “seeing” each other. We will correct this omission in this part.

Starfish supports three types of material interactions: chemical reactions, MCC, and DSMC. The easiest way to differentiate between these is to think of them as fluid-fluid, particle-fluid, and particle-particle events, respectively. Chemical reactions operate solely with the density and temperature fields and are applicable to models described by a rate equation. They are useful for modeling production or destruction of material in processes such as ionization or recombination.

MCC, or Monte Carlo Collisions, are kinetic-fluid interactions. The source material collides with a target cloud. The number density of the target at the particle position is used to determine the collision probability. If the collision occurs, only the source particle is modified. The target is not affected by the collision. As such, momentum is not conserved. MCC is suitable for cases when the target material is sufficiently more dense than the source, such as when a rarefied ion beam interacts with a dense neutral cloud via the Charge Exchange (CEX) collision.

Finally, DSMC (Direct Simulation Monte Carlo) is a kinetic-kinetic collision process. This method collides particles with other particles in the simulation cell. Both energy and momentum are conserved. This method is suitable for modeling collisions in like gases, such as to model momentum exchange (MEX) collisions in the ion gas. Starfish implements the No Time Counter (NTC) method of Bird[1]. DSMC is the most computationally demanding of these three methods.

Specifying Interactions

Material interactions are specified in the interactions file which you have already seen before. We used this file to add surface recombination. We modify the interactions file as follows:

<!-- material interactions file -->
<material_interactions>
 
<!-- surface interaction -->
<surface_hit source="O+" target="SS">
<product>O</product>
<model>cosine</model>
<prob>0.9</prob>
<c_accom>0.5</c_accom>
<c_rest>0.9</c_rest>
</surface_hit>
 
<!-- chemical reaction -->
<chemistry name="ionization" >
<sources>O,e-</sources>
<products>iO+,2*e-</products>
<rate>
 <type>polynomial</type>
 <coeffs>1,0</coeffs>
 <multiplier>1e-9</multiplier>
 <dep_var mat="e-"></dep_var>
</rate>
</chemistry> 
 
<!-- MCC charge exchange -->
<mcc model="cex">
<source>O+</source>
<target>O</target>
<sigma>const</sigma>
<sigma_coeffs>1e-7</sigma_coeffs>
</mcc> 
 
<!-- DSMC momentum exchange -->
<dsmc model="vhs">
<source>O+</source>
<target>O+</target>
<sigma>const</sigma>
<sigma_coeffs>1e-18</sigma_coeffs>
</dsmc> 
 
</material_interactions>

We have added three new interactions types to the list: chemistry, mcc, and dsmc. Of course, you could repeat these definitions to specify multiple collision pairs. We will now go through each interaction type in detail.

Chemical Reactions

The chemistry interaction type models interactions that can be written in terms of density change. As an example, consider the ionization process:
$$O+e^- \rightarrow O^+ +2e^-$$

We can write this process as follows:
$$\begin{array}{rcl}
\text{d}n_{O^+} &=& +k n_{O} n_{e^-} \text{d}t \\
\text{d}n_{O} &=& -k n_{O^+} n_{e^-} \text{d}t
\end{array}$$
ignoring electron density change. Here “k” is the ionization rate (which is typically function of the electron temperature) and the two “n” correspond to the densities of the atoms and electrons. The rate “k” is model-specific, and Starfish supports several different rate models (and you can define your own via plugins). Here we use a simple polynomial model based on the specified material temperature. A more robust method for specifying the dependent variable will be implemented in a future release. Effectively we have a constant reaction rate since only the first coefficient is non-zero. The resulting rate is multiplied by the value of the “multiplier”, and hence this parameter can be used to scale the reaction rate. Since this reaction requires neutrals and electrons, we would expect the ionization to occur only in the region where neutrals are present – i.e. where the ions have recombined with the wall. This is indeed the case as we can see from Figure 1 below. This plot compares the product and reactant densities for two values of the reaction rate multiplier. In the first plot, the multiplier is set high enough that all neutrals ionize. The exception is the thin layer near the surface which is due to incoming ions becoming neutralized in the current time step. This is a numerical artifact that may be corrected in a future version.

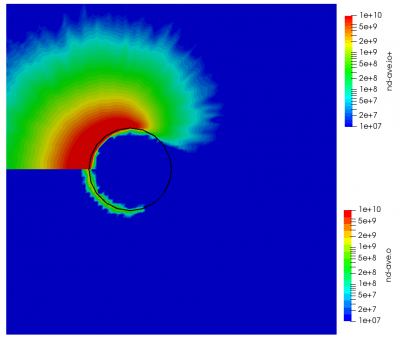
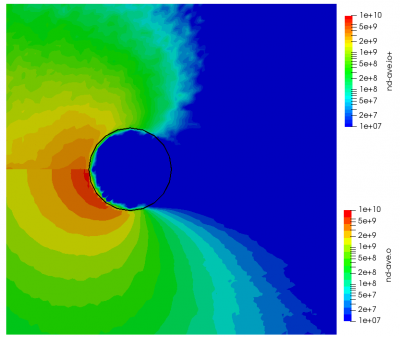
You may have some questions at this point. Such as, where did the electrons come from? In this example we do not simulate electrons directly. Potential is computed assuming electrons follow the Boltzmann relationship. Prior versions of Starfish automatically created a fluid electron population that was based on this relationship. This automatic creation is no longer supported and instead electrons need to be included in the material’s file. The syntax is as follows:

<material name="e-" type="fluid-electrons">
<model>qn</model>
<kTe0>1.5</kTe0>
</material>

This tells the code to introduce a fluid electron population. The density is computed by assuming quasi-neutrality, \(n_e=n_i\). This is inconsistent with the potential solver, but was needed to get enough electron in the deep sheath around the sphere. This population will have a constant temperature of 1.5 eV. We also introduce a new material to capture the ionization product,

<material name="iO+" type="kinetic">
<molwt>16</molwt>
<charge>0</charge>
<spwt>1e3</spwt>
<init>T=10000</init>
</material>

These “ions” are given a non-physical charge of zero for visualization purposes. These particles will be created in the sheath with thermal velocity at 10,000K and as such, would not have enough energy to escape the potential well.

Finally, you may also be wondering how the change in density works with kinetic materials. The “dn” is converted into a volumetric source. After the density changes are computed for all chemical reactions, Starfish loops through the cells and creates in each cell as many particles as needed to satisfy the new density increase. The particles are created randomly in the cell and have initial velocity corresponding the Maxwellian distribution at the target gas temperature. This process will create particles with specific weights less than the default one prescribed in the materials.xml file. Similarly, negative densities are used to destroy particles. The density is converted to a number loss, and random particles from the cell are destroyed until enough are removed. If the remaining mass loss is less than a mass of a single macroparticle, the specific weight of a particle is reduced accordingly.

MCC

Let’s now move onto MCC, which was described in more detail in a previous article. To specify MCC interactions, we add the following to the list of interactions

<mcc model="cex">
<source>O+</source>
<target>O</target>
<sigma>const</sigma>
<sigma_coeffs>1e-7</sigma_coeffs>
</mcc>

Just as in the case of the chemical reaction, we specify the source and target, as well as the collision model. In this case, we’ll be using the CEX handler. This handler models the electron exchange between a fast ion and a slow neutral resulting in a fast neutral and a slow ion,
$$O^+_{fast} + O_{slow} \rightarrow O_{fast} + O^+_{slow}$$

But since this is MCC, we don’t actually modify the neutrals. Instead, the neutrals are used to compute the collision probability following \(P=1-\exp(-n_ng\sigma\Delta t)\), where \(n_n\) is the neutral density, \(g\) is the relative velocity between the ion and the neutral (with the neutral assumed to be stationary), and \(\sigma\) is the collision cross-section. The sigma model is typically a function of relative velocity, with a number of models existing to describe different collision events. A classic model for modeling CEX is the model of Rapp and Francis. However here, for simplicity, we use a constant cross-section. This cross-section is many orders of magnitude higher than a typical CEX cross-section. This extremely large value was chosen just to demonstrate the effect.

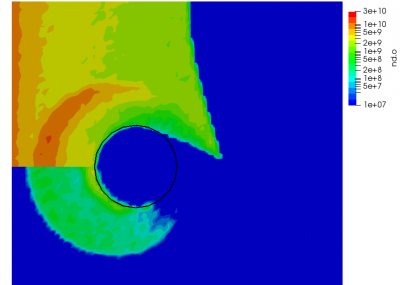
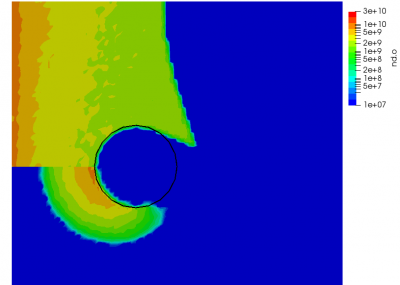
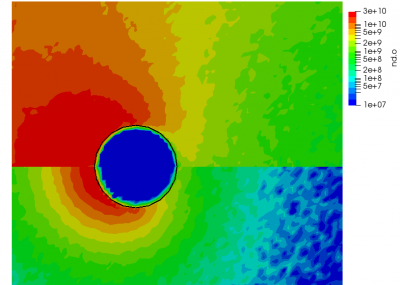
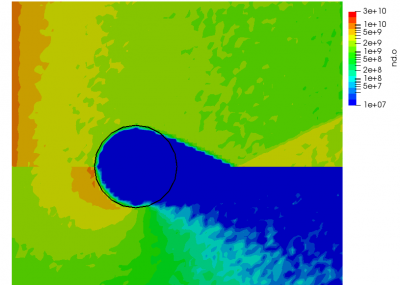
We can also further study the collisional behavior by adding an mcc-nu variable to the output. This data is visualized below.

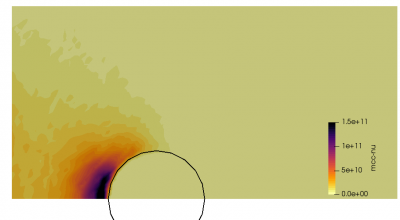
DSMC

DSMC is demonstrated in more detail in a separate tutorial.

References

[1] Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows, Oxford Science Publications, 2003
[2] Fife, J., Hybrid-PIC Modeling and Electrostatic Probe Survey of Hall Thrusters, Ph.D. Dissertation, Massachusetts Institute of Technology, 1998.